When you look around at the world, you see patterns everywhere. From the ripples on the surface of a pond to the branches of a tree, the natural world is full of intricate, repeating shapes that catch the eye and spark the imagination.
But have you ever thought about how these patterns are created? How does a simple process like the flow of water or the growth of a plant lead to such complex and beautiful structures?
Understanding Cellular Automata: A Brief Overview
The mathematical concept called Cellular Automata is a way of modeling the behavior of simple units, or “cells,” that interact with each other based on a set of rules. When these cells follow these rules over and over again, they can create stunning patterns that look almost like works of art.
For example, imagine a grid of cells, where each cell can be either “on” or “off.” We start by turning on a single cell, and then let the cells evolve over time according to some simple rules. Perhaps a cell will turn on if its neighbors are also on, or turn off if they are off. Maybe the cells will switch their state if there are too many or too few neighbors of a certain type.
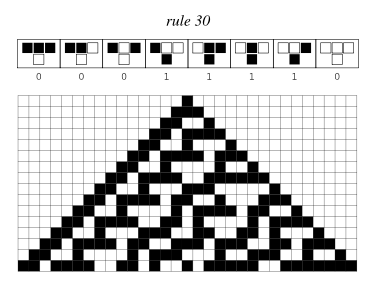
Stephen Wolfram coined the term “elementary cellular automata” to refer to binary, nearest-neighbor, one-dimensional automata – the most basic type. He has thoroughly investigated their remarkable characteristics.
Image: mathworld.wolfram.com
By representing each generation in a different row, the process of a one-dimensional cellular automaton’s evolution can be visualized, as shown in the image above, which displays the first 20 generations of an elementary cellular automaton with rule 30, originating from a solitary black cell.
Since there are 2x2x2 = 8 possible binary states for the three cells neighboring a given cell, there are a total of 28 = 256 elementary cellular automata.
Image: mathworld.wolfram.com

As we watch the cells change and interact with each other, we begin to see patterns emerge. There might be swirling spirals or branching tendrils, checkerboard grids or chaotic clouds. And the beauty of Cellular Automata is that these patterns can be incredibly varied and complex, even though they arise from such simple rules.
Applications of Cellular Automata
In fact, Cellular Automata have been used to model all sorts of natural phenomena, from the behavior of flocks of birds to the growth of crystals. By studying these patterns, scientists and mathematicians have gained new insights into how the world works and what makes it so endlessly fascinating.
Biology:
Cellular automata have been used to model various biological phenomena with simple state spaces. Examples include the patterns on some seashells, where pigment cells in a narrow band along the shell’s lip secrete pigments according to the activating and inhibiting activity of their neighbor pigment cells, leaving colored patterns on the shell as it grows.
Plants also regulate their intake and loss of gases via a cellular automaton mechanism, with each stoma on the leaf acting as a cell.
Moving wave patterns on the skin of cephalopods can be simulated with a two-state, two-dimensional cellular automaton, with each state corresponding to either an expanded or retracted chromatophore.
Threshold automata have been invented to simulate neurons, and complex behaviors such as recognition and learning can be simulated.
Chemistry:
The Belousov-Zhabotinsky chemical reaction, which produces intriguing geometric patterns, can be simulated with a cellular automaton.
Physics:
Probabilistic cellular automata are used in physics to study fluid dynamics and phase transitions. The Ising model is a well-known example, which represents a magnet using two states: “up” and “down”. By adjusting the model parameters, researchers can vary the proportion of cells being in the same state, revealing how ferromagnets become demagnetized when heated. This has implications for other phase transitions, like evaporation. Lattice gas automata are also significant, as they simulate fluid flows.
Computing:
Cellular automaton processors use identical cells in a regular grid to process information, and can interact via various means without the need for wires. They can also be used for cryptography and solving various problems such as error correction and the majority problem.
Generative Art (visual / music):
By using Cellular Automata, artists can produce complex and intricate patterns and shapes that would be difficult to create by hand. These patterns can then be used as the basis for further artistic experimentation, such as adding color, texture, or other design elements.
Nicu P has been incorporating cellular automata directly into his generative artworks, using the patterns generated by these systems as a key component of the composition and texture.
Play with it live: Clockwork Orange (infinite variations)
Play with it live: The Old Pond (infinite variations)
Play with it live: Ask the mushroom (infinite variations)
References: